How is the product (and its unique map) related to terminal objects?
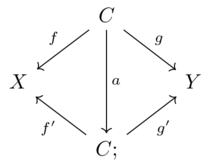
Call \(\mathbf{Cone}(X,Y)\) the /category of cones over X and Y in/ \(\mathcal{C}\), given two objects in \(\mathcal{C}\).
An object is pair of maps \(X \xleftarrow{f}C\xrightarrow{g}Y\) for some \(c \in \mathcal{C}\)
A morphism a from \(X \xleftarrow{f}C\xrightarrow{g}Y\) to \(X \xleftarrow{f'}C\xrightarrow{g'}Y\) is a morphism \(C \rightarrow C'\) in \(\mathcal{C}\) such that the following diagram commutes: